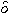 -equations on certain unbounded weakly pseudo convex domains, Transactions
of American Math. Soc. 1989, p.389-413
-equations on certain unbounded weakly pseudo convex domains, Transactions
of American Math. Soc. 1989, p.389-413List of Publications and Preprints
updated on Jan. 2, 2024
Preprints
S. Fukushima and H. Kang, Decompositions of surface vector fields and topological characterizations of the codimensions, arXiv:2311.14256
H. Kang and D. Kawagoe, Surface Riesz transforms and spectral property of elastic Neumann--Poinca\'e operators on less smooth domains in three dimensions, arXiv:1806.02026
H. Kang, G.W. Milton and J.-N. Wang, Equivalence of inverse problems for 2D elasticity and for the thin plate with finite measurements and its applications, arXiv 1203.3833
in Press
K. Ando, H. Kang, Y. Miyanishi, and M. Putina, Generic properties of the Neumann-Poincar\'e operator: simplicity of eigenvalues and cyclic vectors, Ann. Sc. Norm. Super. Pisa Cl. Sci., to appear. arXiv:2312.11916
2025
[1] S. Fukushima, Y.-G. Ji, H. Kang, and X. Li, Finiteness of the stress in presence of closely located inclusions with imperfect bonding, Math. Annalen, 391 (2025), 1753--1778.
[2] K. Ando, H. Kang, Y. Miyanishi, and M. Putina, Carleman factorization of layer potentials on smooth domains, Arch. Rati. Mech. Anal, (2025) 249:35.
2024
[1] S. Fukushima, Y.-G. Ji, and H. Kang, A decomposition theorem of surface vector fields and spectral structure of the Neumann-Poincar\'e operator in elasticity, Trans. Am. Math. Soc., 377 (3) (2024), 2065--2123.
[2] S. Fukushima and H. Kang, Spectral structure of the Neumann-Poincar\'e operator on axially symmetric functions, J Spectr Theory 14 (2024), 1109--1145.
[3] S. Fukushima, H. Kang and Y. Miyanishi, Decay rate of the eigenvalues of the Neumann-Poincar\'e operator, Potential Analysis 61 (2024), 573--596.
2023
[1] H. Kang and S. Sakaguchi, A symmetry theorem in two-phase heat conductors, Mathematics in Engineering, 5(3) (2023), 1--7. doi: 10.3934/mine.2023061
[2] Y.-G. Ji and H. Kang, Spectrum of the Neumann-Poincar\'e operator and optimal estimates for transmission problems in presence of two circular inclusions, Int. Math. Res. Notices 2023(9), 7638--7685, Correction: 2023(7), 6299--6300, https://doi.org/10.1093/imrn/rnac057
[3] Y.-G. Ji and H. Kang, Spectral properties of the Neumann-Poincar\'e operator on rotationally symmetric domains in two dimensions, Math. Annalen 387 (2023), 1105--1123. https://doi.org/10.1007/s00208-022-02482-w
[4} S. Fukushima, Y.-G. Ji, H. Kang and Y. Miyanishi, Spectral properties of the Neumann-Poincar\'e operator and cloaking by anomalous localized resonance: a review, J. Korean Soc. Ind. Appl. Math. 27(2) (2023), 87–108.
[5] H. Ammari, H. Kang, D.W. Kim and S. Yu, Quantitative estimates for stress concentration of the Stokes flow between adjacent circular cylinders, SIAM J. Math. Anal, 55(4) (2023), 3755--3806.
[6] H. Kang, Quantitative analysis of field concentration in presence of closely located inclusions of high contrast, Proceedings ICM 2022, Vol 7, 5680--5701, 2023.
2022
[1] H. Kang, X. Li, and S. Sakaguchi, Existence of weakly neutral coated inclusions of general shape in two dimensions, Appl. Anal., 101(4) (2022), 1330-1353.
[2] H. Kang, Spectral Geometry and Analysis of the Neumann-Poincaré Operator, a Review. In: Kang, NG., Choe, J., Choi, K., Kim, Sh. (eds) Recent Progress in Mathematics. KIAS Springer Series in Mathematics, vol 1. Springer, Singapore. https://doi.org/10.1007/978-981-19-3708-8_4
[3] K. Ando, H. Kang, S. Lee and Y. Miyanishi, Spectral structure of the Neumann--Poincar\'e operator on thin ellipsoids and flat domains, SIAM J. Math. Anal, 54(60 (2022), 6164--6185.
[4] K. Ando, H. Kang and Y. Miyanishi, Spectral structure of the Neumann--Poincar\'e operator on thin domains in two dimensions, J. d'Anal. Math. 146 (2022), 791--800, https://doi.org/10.1007/s11854-022-0206-7
[5] H. Kang, J.Y. Lee, I. Trooshin, On the Determination of a Coefficient of an Elliptic Equation via Partial Boundary Measurement. In: Ruzhansky, M., Wirth, J. (eds) Harmonic Analysis and Partial Differential Equations. Trends in Mathematics. Birkhäuse (2022), Cham. https://doi.org/10.1007/978-3-031-24311-0_12
2021
[1] H. Kang and S. Yu, Singular functions and characterizations of field concentrations: a survey, Anal. Theory Appl. 37 (2021), 102--113.
[2] Y.-G. Ji, H. Kang, X. Li, and S. Sakaguchi, Neutral inclusions, weakly neutral inclusions, and an over-determined problem for confocal ellipsoids, {\sl Geometric Properties for Parabolic and Elliptic PDE's}, Springer INdAM series vol 47, 151--181 (a chapter), 2021, Link
[3] K. Ando, H. Kang, Y. Miyanishi and T. Nakazawa, Surface localization of plasmons in three dimensions and convexity, SIAM J. Appl. Math, 81-3 (2021), 1020--1033.
[4] H. Kang, X. Li, and S. Sakaguchi, Polarization tensor vanishing structure of general shape: Existence for small perturbations of balls, Asymptotic Analysis, 125 (2021), 101--132.
[5] H. Kang and S. Sakaguchi, Large time behavior of temperature in two-phase heat conductors, Jour. Diff. Equ, 303 (2021), 268--276.
[6] K. Ando, H. Kang, Y. Miyanishi and M. Putinar, Spectral analysis of Neumann-Poincar\'e operator, Rev. Roumaine Math. Pures Appl. 66 (2021), 545--575.
2020
[1] H. Kang and S. Yu, A proof of the Flaherty-Keller formula on the effective property of densely packed elastic composites, Cal. Vari. PDE 59 (2020), 22.
[2] H. Kang and K. Yun, Quantitative estimates for enhancement of the field excited by an emitter due to presence of two closely located spherical inclusions, Jour. Diff. Equ. 269 (2020), 2977--3002.
[3] K. Ando, H. Kang and Y. Miyanishi, Convergence rate for eigenvalues of the elastic Neumann--Poincar\'e operator on smooth and real analytic boundaries in two dimensions, Jour Math Pures Appl. 140 (2020), 211--229.
2019
[1] H. Kang and K. Yun, Optimal estimates of the field enhancement in presence of a bow-tie structure of perfectly conducting inclusions in two dimensions, Jour. Diff. Equ. 266 (2019), 5064--5094.
[2] H. Kang and S. Yu, Quantitative characterization of stress concentration in the presence of closely spaced hard inclusions in two-dimensional linear elasticity, Arch. Rati. Mech. Anal. 232 (2019), 121--196.
[3] H. Kang and X. Li, Construction of weakly neutral inclusions of general shape by imperfect interfaces, SIAM J. Appl. Math. 79 (2019), 396--414.
[4] K. Ando, H. Kang, Y. Miyanishi and E. Ushikoshi, The first Hadamard variation of Neumann--Poincar\'e eigenvalues on the sphere, Proc. Amer. Math. Soc. 147 (2019), 1073--1080.
[5] K. Ando, H. Kang and Y. Miyanishi, Elastic Neumann--Poincar\'e operators on three dimensional smooth domains: Polynomial compactness and spectral structure, Int. Math. Res. Notices 2019 (12) (2019), 3883--3900.
[6] H. Kang and K. Yun, Precise estimates of the field excited by an emitter in presence of closely located inclusions of a bow-tie shape, Jour Math Anal Appl 479 (2) (2019), 1670--1707.
[7] H. Kang and K. Yun, Quantitative estimates of the field excited by an emitter in a narrow region between two circular inclusions, Q Appl Math LXXVII (4) (2019), 861--873.
[8] K. Ando, Y. Ji, H. Kang, D. Kawagoe and Y. Miyanishi, Spectral structure of the Neumann--Poincar\'e operator on tori, Ann. I. H. Poincare-AN 36 (2019), 1817--1828.
[9] Y.-G. Ji and H. Kang, A concavity condition for existence of a negative value in Neumann-Poincar\'e spectrum in three dimensions, Proc. Amer. Math. Soc 147 (2019), 3431-3438
2018
[1] K. Ando, H. Kang and Y. Miyanishi, Spectral Structure of Elastic Neumann--Poincar\'e Operators, Journal of Physics, Conference Series 965 (2018), 012027.
[2] K. Ando, Y.-G. Ji, H. Kang, K. Kim and S. Yu, Spectral properties of the Neumann-Poincar\'e operator and cloaking by anomalous localized resonance for the elasto-static system, Euro. J. Appl. Math 29 (2018), 189--225.
[3] H. Kang and M. Putinar, Spectral permanence in a space with two norms, Rev. Mat. Iberoam. 34 (2018), 621--635.
[4] K. Ando, H. Kang and Y. Miyanishi, Exponential decay estimates of the eigenvalues for the Neumann-Poincar\'{e} operator on analytic boundaries in two dimensions, J. Integr. Equ. Appl. 30 (2018), 473--489.
2017
[1] J. Helsing, H. Kang and M. Lim, Classification of spectra of the Neumann--Poincar\'{e} operator on planar domains with corners by resonance, Ann. I. H. Poincare-AN 34 (2017), 991--1011.
[2] T. Feng, H. Kang and H. Lee, Construction of GPT-vanishing structures using shape derivative, J. Comp. Math. 35 (2017), 569--585.
[3] H. Kang, M. Lim and S. Yu, Spectral resolution of the Neumann-Poincar\'{e} operator on intersecting disks and analysis of plasmon resonance, Arch. Rati. Mech. Anal. 226 (2017), 83--115.
[4] K. Ando, H. Kang, K. Kim and S. Yu, Cloaking by anomalous localized resonance for linear elasticity on a coated structure, SIAM J. Math. Anal. 49 (2017), 4232--4250.
2016
[1] K. Ando and H. Kang, Analysis of plasmon resonance on smooth domains using spectral properties of the Neumann-Poincare operator, J,. Math. Anal. Appl. 435 (2016), 162--178.
[2] H. Kang, K. Kim, H. Lee, J. Shin and S. Yu, Spectral properties of the Neumann-Poincar\'e operator and uniformity of estimates for the conductivity equation with complex coefficients, J London Math Soc (2) 93 (2016), 519--546.
[3] H. Kang and E. Kim, Estimation of stress in the presence of closely located elastic inclusions: A numerical study, Contemporary Math. 660 (2016), 45--57.
[4] K. Ando, H. Kang and H. Liu, Plasmon resonance with finite frequencies: a validation of the quasi-static approximation for diametrically small inclusions, SIAM J. Appl. Math. 76 (2016), 731--749.
[5] T. Feng and H. Kang, Spectrum of the Neumann-Poincar\'e operator for ellipsoids and tunability, Integr. Equat. Oper. Th. 84 (2016), 591--599.
[6] J, Eom, H.Kang, G. Nakamura and Y.-C. Wang, Reconstruction of the shear modulus of viscoelastic systems in a thin cylinder: an inversion scheme and experiments, Inverse Problems 32 (2016) 095007 (19pp).
[7] H. Kang, H. Lee and S. Sakaguchi, An over-determined boundary value problem arising from neutrally coated inclusions in three dimensions, Ann. Sc. Norm. Super. Pisa Cl. Sci. (5) XVI (2016), 1193-1208.
[8] H. Kang, On coated inclusions neutral to bulk strain fields in two dimensions, Rend. Istit. Mat. Univ. Trieste 48 (2016), 353--367.
2015
[1] H. Ammari, D. Chung, H. Kang, and H. Wang, Invariance Properties of Generalized Polarization Tensors and Design of Shape Descriptors in Three Dimensions, Appl. Comput. Harmon. A., 38 (2015), 140--147.
[2] H. Kang, H. Lee and M. Lim, Construction of conformal mappings by generalized polarization tensors, Math. Method Appl. Sci., 38 (2015), 1847-1854.
[3] O.K. Lee, H. Kang, J.C. Ye and M. Lim, A non-iterative method for the electrical impedance tomography based on joint sparse recovery, Inverse Problems 31 (2015), 075002 (23 pages)
[4] H. Kang, H. Lee and K. Yun, Optimal estimates and asymptotics for the stress concentration between closely located stiff inclusions, Math. Annalen 363 (2015), 1281--1306.
[5] H. Ammari, H. Dong, H. Kang and S. Kim, On an elliptic equation arising from photo-acoustic imaging in inhomogeneous media, Int. Math. Res. Notices (2015), Vol, 2015, 12105--12113.
2014
[1] H. Kang, G.W. Milton and J.-N. Wang, Bounds on the volume fraction of the two-phase shallow shell using one measurement, J. Elasticity 114 (2014), 41--53.
[2] H. Kang, M. Lim and K. Yun, Characterization of the electric field concentration between two adjacent spherical perfect conductors, SIAM J. Appl. Math. 74 (2014), 125--146.
[3] H. Ammari, T. Boulier, J. Garnier, W. Jing, H. Kang and H. Wang, Target Identification Using Dictionary Matching of Generalized Polarization Tensors, Found. Comput. Math. 14 (2014), 27--62.
[4] H. Ammari, J. Garnier, H. Kang, M. Lim, and S. Yu, Generalized Polarization Tensors for Shape Description, Numerische Math. 126 (2014), 199--224.
[5] H. Kang and H. Lee, Coated inclusions of finite conductivity neutral to multiple fields in two dimensional conductivity or anti-plane elasticity, Euro. J. Appl. Math., 25 (3) (2014), 329--338.
[6] H. Ammari, G. Ciraolo, H. Kang, H. Lee and G.W. Milton, Spectral theory of a Neumann-Poincar\'e-type operator and analysis of anomalous localized resonance II, Contemporary Math. 615, 1--14, 2014.
[7] H. Kang, K. Kim, H. Lee, X. Li and G.W. Milton, Bounds on the size of an inclusion using the translation method for two-dimensional complex conductivity, SIAM J. Appl. Math. 74 (2014), 939--958.
[8] H. Ammari, Y. Deng, H. Kang and H. Lee, Reconstruction of Inhomogeneous Conductivities via Generalized Polarization Tensors, Ann. I. H. Poincare-AN 31 (2014), 877--897.
[9] D. Chung, H. Kang, K. Kim and H. Lee, Cloaking due to anomalous localized resonance in plasmonic structures of confocal ellipses, SIAM J. Appl. Math. 74 (2014), 1691--1707.
[10] H. Kang, Layer potential approaches to interface problems, Inverse problems and imaging, Panoramas et Syntheses 44, Societe Mathematique de France, 2014
2013
[1] H. Kang, M. Lim and K. Yun, Asymptotics and Computation of the Solution to the Conductivity Equation in the Presence of Adjacent Inclusions with Extreme Conductivities, J Math Pures Appl., 99 (2013), 234--249.
[2] H. Ammari, H. Kang, H. Lee, and M. Lim, Enhancement of Near Cloaking Using Generalized Polarization Tensors Vanishing Structures. Part I: The Conductivity Problem, Comm Math. Phys., 317 (2013), 253--266.
[3] H. Ammari, H. Kang, H. Lee, and M. Lim, Enhancement of near-cloaking. Part II: the Helmholtz equation, Comm Math. Phys., 317 (2013), 485--502.
[4] H. Ammari, G. Ciraolo, H. Kang, H. Lee and K. Yun, Spectral analysis of the Neumann-Poincar\'e operator and characterization of the stress concentration in anti-plane elasticity, Arch. Rati. Mech. Anal., 208 (2013), 275--304.
[5] H. Kang and G.W. Milton, Bounds on the volume fractions of two materials in a three dimensional body from boundary measurements by the translation method, SIAM J. Appli. Math. 73 (2013), 475--492.
[6] H. Ammari, G. Ciraolo, H. Kang, H. Lee and G.W. Milton, Spectral theory of a Neumann-Poincar\'e-type operator and analysis of cloaking due to anomalous localized resonance, Arch. Rati. Mech. Anal. 208 (2013), 667-692.
[7] H. Ammari, G. Ciraolo, H. Kang, H. Lee and G.W. Milton, Anomalous localized resonance using a folded geometry in three dimensions, Proc. R. Soc. A 469 (2013), 20130048.
[8] H. Ammari, H. Kang, K. Kim and H. Lee, Strong convergence of the solutions of the linear elasticity and uniformity of asymptotic expansions in the presence of small inclusions, Jour. Diff. Equ. 254 (12) (2013), 4446-4464.
[9] H. Ammari, P. Garapon, F. Jouve, H. Kang, M. Lim and S. Yu, A New Optimal Control Approach for the Reconstruction of Extended Inclusions, SIAM J. on Control and Optim. 51(2) (2013), 1372--1394.
[10] H. Ammari, H. Kang, H. Lee and J. Lim, Boundary perturbations due to the presence of small linear cracks in an elastic body, J. Elasticity 113 (1) (2013), 75--91.
[11] H. Ammari, T. Boulier, J. Garnier, H. Kang, and H. Wang, Tracking of a Mobile Target Using Generalized Polarization Tensors, SIAM J. Imaging Sci. 6(3) (2013), 1477--1498.
[12] H. Ammari, H. Kang, H. Lee, M. Lim and S. Yu, Enhancement of near cloaking for the full Maxwell equations, SIAM J. Appl. Math. 73 (2013), 2055-2076.
[13] H. Ammari, E. Bretin, J. Garnier, H. Kang and A. Wahab, Localization, Stability, and Resolution of Topological Derivative Based Imaging Functionals in Elasticity, SIAM J. Imag. Sci. 6 (2013), 2174--2212.
2012
[1] H. Ammari, H. Kang, M. Lim, and H. Zribi, The Generalized Polarization Tensors for Resolved Imaging. Part I: Shape Reconstruction of a Conductivity Inclusion, Math. Comp. 81 (2012), 367-386
[2] H. Ammari, K. Kalimeris, H. Kang, and H. Lee, Layer Potential Techniques for the Narrow Escape Problem, Jour Math Pures Appl., 97 (2012), 66-84.
[3] H. Ammari, J. Garnier, V. Jugnon, and H. Kang, Stability and Resolution Analysis for a Topological Derivative Based Imaging Functional, SIAM Journal on Control and Optimization, 50 (2012), 48-76.
[4] H. Ammari, H. Kang, E. Kim, and J.-Y. Lee, The Generalized Polarization Tensors for Resolved Imaging. Part II: Shape and Electromagnetic Parameters Reconstruction of an Electromagnetic Inclusion from Multistatic Measurements, Math. Comp., 81(278) (2012), 839-860.
[5] H. Ammari, J. Garnier, H. Kang, M. Lim, and K. Solna, Multistatic Imaging of Extended Targets, SIAM Journal on Imaging Sciences, 5 (2) (2012), 564-600.
[6] H. Ammari, H. Kang, and S. Kim, Sharp estimates for the Neumann functions and applications to quantitative photo-acoustic imaging in inhomogeneous media, Jour. Diff. Equa. 25 (2012), 41-72.
[7] H. Ammari, J. Garnier, V. Jugnon, H. Kang, H. Lee, and M. Lim, Enhancement of near-cloaking. Part III: Numerical simulations, statistical stability, and related questions, in Multi-scale and high-contrast PDE: from modelling, to mathematical analysis, to inversion (Ammari, Capdeboscq and Kang, Eds), Contemporary Math. 577 (2012), 1-24.
[8] H. Kang, E. Kim and G. W. Milton, Sharp bounds on the volume fractions of two materials in a two-dimensional body from electrical boundary measurements: the translation method, Cal. Vari. PDE 45 (2012), 367-401.
[9] H. Ammari, P. Garapon, H. Kang, and H. Lee, Effective Viscosity Properties of Dilute Suspensions of Arbitrarily Shaped Particles, Asymptotic Analysis 80 (2012), 189-211.
2011
[1] H. Ammari, J. Garnier, H. Kang, W.-K. Park, and K. Solna, Imaging schemes for perfectly conducting cracks, SIAM J. Appl. Math., 71(1) (2011), 68-91. Link
[2] H. Ammari and H. Kang, Expansion Methods, Handbook of Mathematical Mehtods of Imaging, 447-499, Springer, 2011.
[3] H. Ammari, H. Kang, E. Kim, M. Lim, and K. Louati, A Direct Algorithm for Ultrasound Imaging of Internal Corrosion, SIAM J. Numer. Anal. 49 (2011), 1177-1193.
[4] H. Ammari, J. Garnier, H. Kang, H. Lee, and K. Solna, The mean escape time for a narrow escape problem with multiple switching gates, SIAM Multi. Model. Simul. 9 (2011), 817-833.
[5] H. Ammari, E. Bossy, V. Jugnon, and H. Kang, Reconstruction of the Optical Absorption Coefficient of a Small Absorber from the Absorbed Energy Density, SIAM Jour. Appl. Math. 71 (2011), 676-693.
[6] H. Ammari, J. Garnier, V. Jugnon, and H. Kang, Direct reconstruction methods in ultrasound imaging, Mathematical Modeling in Biomedical Imaging II: Optical, Ultrasound, and Opto-Acoustic Tomographies. Lecture Notes in Mathematics: Mathematical Biosciences Subseries, Volume 2035, 29-52, Springer-Verlag, Berlin, 2011.
[7] H. Ammari, L. Guadarrama Bustos, H. Kang, and H. Lee, Transient Elasticity Imaging and Time Reversal, Proc. Royal Soc. Edin, 141 (2011), 1121-1140.
[8] H. Ammari, M. Asch, L. Guadarrama Bustos, V. Jugnon, and H. Kang, Transient wave imaging with limited-view data, SIAM Journal on Imaging Sciences, 4 (2011), 1097-1121.
2010
[1] H. Ammari, H. Kang, M. Lim, and H. Zribi, Conductivity Interface Problems. Part I: Small Perturbations of an Interface, Trans. Amer. Math. Soc., 362 (2010), 2435-2449. Link
[2] H. Ammari, H. Kang, M. Lim, and H. Zribi, Layer Potential Techniques in Spectral Analysis. Part I: Complete Asymptotic Expansions for Eigenvalues of the Laplacian in Domains with Small Inclusions, Trans. Amer. Math. Soc., 363 (2010), 2901-2922. Link
[3] H. Ammari, H. Kang, H. Lee, and W.-K. Park, Asymptotic Imaging of Perfectly Conducting Cracks, SIAM Jour. Sci. Comput. 32 (2) (2010), 894-922. Link
[4] H. Ammari. E. Beretta, E. Francini, H. Kang, M. Lim, Optimization algorithm for reconstructing interface changes of a conductivity inclusion from modal measurements, Math. Comp. 79 (2010), 1757-1777. Link
[5] H. Ammari, Y. Capdeboscq, H. Kang, H. Lee, G. W. Milton, and H. Zribi, Progress on the strong Eshelby's Conjecture and Extremal Structures for the Elastic Moment Tensor, Jour Math Pures Appl. 94 (2010), 93-106. Link
[6] H. Ammari, P. Garapon, L. Guadarrama Bustos, and H. Kang, Transient anomaly imaging by the acoustic radiation force, Jour. Diff. Equa., 249 (7) (2010), 1579-1595. Link
[7] H. Ammari. E. Beretta, E. Francini, H. Kang, and M. Lim, Reconstruction of small interface changes of an inclusion from modal measurements II: The elastic case, Jour Math Pures Appl. 94 (2010), 322-339. Link
[8] H. Ammari, E. Bossy, V. Jugnon, and H. Kang, Mathematical Modelling in Photo-Acoustic Imaging, SIAM Rev. 52 (2010), 677-695. Link
2009
[1] H. Ammari, H. Kang, E. Kim, H. Lee, and K. Louati, Vibration Analysis for Detecting Internal Corrosion, Stud. Appl. Math., 122(1) (2009), 85-104. Link
[2] H. Kang, Conjectures of Polya-Szego and Eshelby, and the Newtonian Potential Problem; A Review, Mechanics of Materials, 41 (2009), 405-410. Link
[3] H. Ammari, H. Kang, E. Kim, and H. Lee, Vibration testing for anomaly detection, Math. Meth. Appl. Sci. 32 (7) (May, 2009), 863-874. Link
[4] H. Ammari, H. Kang, and E. Kim, Detection of Internal Corrosion, ESAIM: Proc., April 2009, Vol 26, 207-216. Link
[5] H. Ammari, Y. Capdeboscq, H. Kang, and A. Kozhemyak, Mathematical models and reconstruction methods in Magneto-acoustic imaging, Euro. Jour. Appl. Math., 20 (2009), 303-317. Link
[6] H. Ammari, H. Kang, and H. Lee, Asymptotic Analysis of High-Contrast Phononic Crystals and a Criterion for the Band-Gap Opening, Arch. Rational Mech. Anal., 193 (2009), 679-714. Link
[7] H. Ammari, H. Kang, H. Lee, M. Lim, and H. Zribi, Decomposition Theorems and Fine Estimates for Electrical Fields in the Presence of Closely Located Circular Inclusions, Jour. Diff. Equa., 247 (2009), 2897-2912. Link
[8] H. Ammari and H. Kang, The Method of Small-Volume Expansions for Medical Imaging, Lecture Notes in Math. Vol. 1983, Chap. 3, 99-132, 2009, Springer, New York.
2008
[1] H. Ammari, H. Kang, E. Kim, K. Louati, and M.S. Vogelius, A MUSIC-type Algorithm for Detecting Internal Corrosion from Electrostatic Boundary Measurements, Numer. Math. 108 (Feb. 2008), 501-528. Link
[2] H. Kang and G.W. Milton, Solutions to the Polya-Szego Conjecture and the Weak Eshelby Conjecture, Arch. Rational Mech. Anal, 188 (2008), 93-116. Link
[3] H. Ammari, P. Garapon, H. Kang, and H. Lee, A Method of Biological Tissues Elasticity Reconstruction Using Magnetic Resonance Elastography Measurements, Quar. Appl. Math., 66 (2008) 139-175.
[4] Y. Capdeboscq and H. Kang, Improved Hashin-Shtrikman Bounds for Elastic Moment Tensors and an Application, Applied Math. Optimization 57 (2008), 263-288. Link
[5] H. Kang, E. Kim, and G.W. Milton, Inclusion pairs satisfying Eshelby's uniformity property, SIAM J. Appl. Math. 69 (2008), 577-595. Link
2007
[1] H. Ammari, H. Kang, and H. Lee, A Boundary Integral Method for Computing Elastic Moment Tensors for Ellipses and Ellipsoids, Jour. Comp. Math., 25 (1) (Jan. 2007), 2-12.
[2] H. Kang and K. Kim, Anisotropic Polarization Tensors for Ellipses and Ellipsoids, Jour. Comp. Math., 25 (2) (Mar. 2007), 157-168.
[3] H. Ammari, G. Dassios, H. Kang, and M. Lim, Estimates for the electric field in the presence of adjacent perfectly conducting spheres, Quat. Appl. Math. 65 (July, 2007), 339-355. Link
[4] H. Ammari, H. Kang, and H. Zribi, Sensitivity Analysis with respect to the electrical conductivity, J. Comp. Math. 25(3) (May, 2007), 244-251. Link
[5] Y. Daido, H. Kang, and G. Nakamura, A probe method for the inverse boundary value problem of nonstationary heat equations, Inverse Problems 23 (Oct. 2007), 1787-1800. Link
[6] H. Kang, E. Kim, and J.-Y. Lee, Numerical Reconstruction of a Cluster of Small Elastic Inclusions, Inverse Probelms 23 (6) (Dec. 2007), 2311-2324. Link
[7] H. Ammari, H. Kang, H. Lee, J. Lee, and M. Lim, Optimal Estimates for the Electrical Field in Two Dimensions, J. Math. Pures Appl. 88 (2007), 307-324. Link
[8] H. Ammari, H. Kang, and H. Lee, Asymptotic Expansions for Eigenvalues of the Lam\'{e} System in the Presence of Small Inclusions, Comm in PDE 32 (Nov. 2007), 1715-1736. Link
2006
[1] H. Ammari, H. Kang, and K. Touibi, An asymptotic formula for the voltage potential in the case of a near-surface conductivity inclusion, Zeitschrift für Angewandte Mathematik und Physik (ZAMP), 57 (Mar. 2006), 234-243. Link
[2] H. Ammari, H. Kang, and M. Lim, Effective Parameters of Elastic Composites, Indiana Univ. Math. J. 55, No. 3 (May, 2006), 903-922. Link
[3] H. Ammari, H. Kang, S. Soussi, and H. Zribi, Layer Potential Techniques in Spectral Analysis. Part II: Sensitivity Analysis of Spectral Properties of High Contrast Band-Gap Materials, SIAM Multi. Model. Simul., 5 (2) (April, 2006), 646-663. Link
[4] H. Ammari and H. Kang, Reconstruction of Elastic Inclusions of Small Volume via Dynamic Measurements, Applied Math. and Optimization, 54 (2) (Sept. 2006), 223-235. Link
[5] H. Ammari, Y. Capdeboscq, H. Kang, E. Kim, and M. Lim, Attainability by Simply Connected Domains of Optimal Bounds for Polarization Tensors, European Jour. of Applied Math. 17 (2) (April, 2006), 201-219. Link
[6] H. Ammari and H. Kang, Generalized Polarization Tensors, Inverse Conductivity Problems, and Dilute Composite Materials: A Review, in Inverse Problems, Multi-scale Analysis and Effective Medium Theory (H. Kang and H. Ammari Eds), Contemporary Math. 408 (2006), 1-67.
[7] Y. Capdeboscq and H. Kang, Improved Bounds on the Polarization Tensor for Thick Domains, in Inverse Problems, Multi-scale Analysis and Effective Medium Theory (H. Kang and H. Ammari Eds), Contemporary Math. 408 (2006), 69-74.
[8] H. Kang and G.W. Milton, On Conjectures of Polya-Szego and Eshelby, in lnverse Problems, Multi-scale Analysis and Effective Medium Theory (H. Kang and H. Ammari Eds), Contemporary Math. 408 (2006), 75-80.
[9] H. Ammari, H. Kang, and E. Kim, Approximate Boundary Conditions for Patch Antennas Mounted on Thin Dieletric Layers, Commun. Comput. Physics, Vol 1, No. 6 (Dec. 2006), 1076-1095.
[10] H. Ammari, H. Kang, and F. Santosa, Scattering of electromagnetic waves by thin dielectric planar structures, SIAM J. Math. Anal., 38 (4) (Dec. 2006), 1329-1342. Link
2005
[1] H. Ammari, H. Kang, and K. Touibi, Boundary Layer Techniques for Deriving the Effective Properties of Composite Materials, Asymptotic Analysis, Vol 41, no. 2 (Feb, 2005), pp. 119-140, PDF file
[2] H. Kang and K. Tanuma, An Inverse Problem for Scalar Conservation Laws, Inverse Problems 21 (June, 2005), 1047-1059. Link
[3] H. Ammari, H. Kang, E. Kim, and M. Lim, Reconstruction of Closely Spaced Small Inclusions, SIAM Journal on Numerical Analysis Vol 42, No. 6 (Mar, 2005), 2408-2428. Link
[4] H. Ammari, H. Kang, and K. Kim, Polarization Tensors and Effective Properties of Anisotropic Composite Materials, Jour. of Differential Equations 215 (Sept, 2005), 401-428, Link
[5] H. Ammari, H. Kang, and M. Lim, Gradient Estimates for Solutions to the Conductivity Problem, Math. Ann. 332(2) (June, 2005), 277-286. Link
[6] H. Ammari, E. Iakovleva, and H. Kang, Reconstruction of a small inclusion in a 2-D open waveguide, SIAM Jour. of Applied Math., Vol. 65, No. 6 (Aug, 2005), 2107-2127. Link
[7] H. Ammari, M. Asch, and H. Kang, Boundary voltage perturbations caused by small conductivity inhomogeneities nearly touching the boundary, Advances in Appl. Math., 35 (Oct, 2005), 368-391. Link
[8] H. Ammari, H. Kang, and M. Lim, Polarization Tensors and Their Applications, Journal of Physics: Conference Series, 12 (2005), 13-22. Link
[9] H, Kang, G. Nakamura, and M. Lim, Reconstruction of polygonal cavities by two boundary measurements, Journal of Physics: Conference Series, 12 (2005), 75-82. Link
[10] H. Ammari, E. Iakovleva, H. Kang, and K. Kim, A direct algorithm for thermal imaging of small inclusions, SIAM J. Multiscale Modeling and Simulation 4 (Oct. 2005), 1116-1136. Link
2004
[1] H. Kang and G. Uhlmann, Inverse problems for the Pauli Hamiltonian in two dimensions, Journal of Fourier Analysis and Applications 10 (2) (Mar. 2004), 201-215. Link
[2] H. Ammari and H. Kang, Reconstruction of Conductivity Inhomogeneities of Small Diameter via Boundary Measurements, Contemporary Math. 348, 23-32.
[3] H. Ammari and H. Kang, Boundary Layer Techniques for Solving the Helmholtz Equation in the Presence of Small Inhomogeneities, Journal of Mathematical Analysis and Application, 296 (Aug. 2004), 190-208. Link (IF=0.444, Elsevier)
[4] H. Kang and H. Lee, Identification of Simple Poles via Boundary Measurements and an Application to EIT, Inverse Problems, 20 (Dec. 2004), 1853-1863. Link (IF=1.248, IOP)
[5] H. Ammari and H. Kang, Sur le problème de conductivité inverse. (French) [On the inverse conductivity problem] Séminaire: Équations aux Dérivées Partielles. 2003--2004, Exp. No. XIII, 15 pp., École Polytech., Palaiseau, 2004. MR2117045
2003
[1] H. Kang and K. Yun, Boundary determination of conductivities and Riemannian metrics via local Dirichlet-to-Neumann operator, SIAM Jour. Math. Anal., Vol. 34, No. 3 (May, 2003), 719-735
[2] H. Ammari and H. Kang, High-Order Terms in the Asymptotic Expansions of the Steady-State Voltage Potentials in the Presence of Conductivity Inhomogeneities of Small Diameter, SIAM J. Math. Anal., Vol. 34, No. 5 (Sept, 2003), 1152-1166.
[3] H. Kang, E Kim, and K. Kim, Anisotropic polarization tensors and detection of an anisotropic inclusion, SIAM J. Appl. Math., Vol. 63, No. 4 (July, 2003), 1276-1291.
[4] H. Kang, E. Kim, and J. Lee, Identification of Elastic Inclusions and Elastic Moment Tensors by Boundary Measurements, Inverse Problems 19 (June, 2003), 703-724.
[5] H. Ammari and H. Kang, Properties of the generalized polarization tensors, SIAM J. Multiscale Modeling and Simulation, Vol 1, No. 2 (April, 2003), 335-348
[6] H. Kang, M. Lim, and G. Nakamura, Detection of Surface Breaking Cracks in Two Dimensions, Inverse Problems 19 (Aug. 2003), 909-918. Link
2002
[1] H. Kang and G. Nakamura, Identification of nonlinearity in a conductivity equation via the Dirichlet-to-Neumann map, Inverse Problems 18 (Aug. 2002), 1079-1088
[2] H. Kang, A uniqueness theorem for an inverse boundary value problem in two dimensions, Jour. Math. Anal. Appl. 270 (June, 2002), 291-302
[3] H. Ammari, H. Kang, G. Nakamura, and K. Tanuma, Complete Asymptotic Expansions of Solutions of the System of Elastostatics in the Presence of an Inclusion of Small Diameter and Detection of an Inclusion, Jour. of Elasticity, 67 (May, 2002), 97-129.
[4] H. Ammari and H. Kang, A new method for reconstructing electromagnetic inhomogeneities of small volume, Inverse Problems 19 (Feb. 2003), 63-71
[5] H. Ammari, H. Kang, G. Nakamura, and K. Tanuma, Asymptotic Expansion of Solutions to the Lam\'e System in the Presence of Inclusions and Applications, Proceedings of International conference on Structual Stability and Dynamics (2002), 755-761
2001
[1] H. Kang and H. Koo, Estimates of the harmonic Bergman kernel on smooth domains, Jour. of Functional Analysis 185 (2001), 220-239
[2] H. Kang and J.-K. Seo, A note on uniqueness and stability in the inverse conductivity problem with one measurement, Jour. of Korean Math. Soc. 38 (2001), 781-791
[3] 강현배, 서진근, 역전도체 문제와 전기 임피던스 영상 기법, Comm. of Korean Math. Soc, 16 (2001), 333-369
2000
[1] H. Kang and H. Koo, Two-weighted inequalities for the derivatives of holomorphic functions and Carleson measures on the unit ball, Nagoya Math. J. Vol 158 (2000), 107-132
[2] H. Kang and J.-K. Seo, Recent Progress in the inverse conductivity problem with single measurement, in Inverse problems and related fields, CRC Press, 2000
[3] H. Kang, K. Kwon, and K. Yun, Recovery of an inhomogeneity in an elliptic equation, Inverse Problems 17 (2001) 25-44
1999
[1] E. Fabes, H. Kang and J.-K. Seo, The inverse conductivity problem with one measurement: error estimates and approximate identification for perturbed disks, SIAM J. of Math. Anal, Vol 30, No. 4 (1999), pp. 699-720
[2] H. Kang and J.-K. Seo, The inverse conductivity problem with one measurement: uniqueness for balls", SIAM J. of Applied Math. Vol 59, No.5 (1999), pp. 1533-1539
[3] H. Kang and J.-K. Seo, Identification of domains with near-extreme conductivity: global stability and error estimates", Inverse Problems 15 (1999) 851-867
1997
[1] H. Kang and H. Koo, Carleson measure characterizations of BMOA on pseudoconvex domains, Pacific J. of Math., 178(2) (1997), 279-291
[2] H. Kang, J.-K. Seo, and D. Sheen, Numerical Identification of Discontinuous Conductivity Coefficients, Inverse Problems, 13 (1997), 113-123
[3] H. Kang, J.-K. Seo, and D. Sheen, The inverse conductivity problem with one measurement: stability and estimation of size, SIAM J. of Math. Anal, 28(6) (1997), 1389-1405
[4] H. Kang and J.-K. Seo, On stability of a transmission problem, Jour. Korean Math. Soc., 34 (1997), 695-706
before 1996
[1] H. Kang, 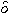 -equations on certain unbounded weakly pseudo convex domains, Transactions
of American Math. Soc. 1989, p.389-413
-equations on certain unbounded weakly pseudo convex domains, Transactions
of American Math. Soc. 1989, p.389-413
[2] H. Kang, An approximation theorem for Szego kernels and applications, Michigan Math. Jour. 1990, p.447-458
[3] H. Kang, On the Fourier transform of  , Studia Math, 1991, p.231-234
, Studia Math, 1991, p.231-234
[4] H. Kang and J.-K. Seo, L2-boundedness of Cauchy transforms on smooth non-Lipschitz curves, Nagoya Math. J. 130 (1993), 123-147.
[5] H. Kang, Automorphism groups on certain class of Reinhardt domains, Bull of KMS 30 (1993), 171-177
[6] H. Kang, J.-K. Seo, and Y.S. Shim, On the restriction of BMO, Jour of KMS 31 (1994), 703-707
[7] Y. Ha, H. Kang, J. Lee, and J.-K. Seo, Unimodular wavelets for and the Hardy space, Michigan Math. J. 41 (1994), 345-361
[8] H. Kang, On holomorphic automorphisms on certain class of domains of infinite type, Tohoku Math. J. 46 (1994), 435-442
[9] H. Kang and J.-K. Seo, Cauchy transforms on polynomial curves and related operators, Nagoya Math. J., Vol 138 (1995), 19-32
[10] H. Kang and H. Koo, A note on BMOA and VMOA on the unit ball, Complex Vari., 29 (1996), 225-231
[11] H. Kang and J-K. Seo, Layer potential techniques for the inverse conductivity problems, Inverse Problems, 12 (1996), 267-278